|
|||||||||||||||||||||
| Process capability compares the output of an in-control process to the specification limits by using capability indices. The comparison is made by forming the ratio of the spread between the process specifications (the specification "width") to the spread of the process values, as measured by 6 process standard deviation units (the process "width"). Process Capability Indices | |||||||||||||||||||||
| A process capability index uses both the process variability and the process specifications to determine whether the process is "capable" |
We are often required to compare the output of a stable process with
the process specifications and make a statement about how well the process
meets specification. To do this we compare the natural variability
of a stable process with the process specification limits.
A process where almost all the measurements fall inside the
specification limits is a capable process.
This can be represented pictorially
by the plot below:
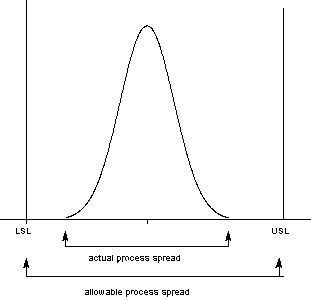
There are several statistics that can be used to measure the capability of a process: Cp, Cpk, Cpm. Most capability indices estimates are valid only if the sample size used is 'large enough'. Large enough is generally thought to be about 50 independent data values. The Cp, Cpk, and Cpm statistics assume that the population of data values is normally distributed. Assuming a two-sided specification, if 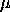 and and
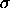 are the mean
and standard deviation, respectively, of the normal data and
USL, LSL, and T are the upper and lower specification limits and the
target value, respectively,
then the population capability indices are defined as follows: are the mean
and standard deviation, respectively, of the normal data and
USL, LSL, and T are the upper and lower specification limits and the
target value, respectively,
then the population capability indices are defined as follows:
|
||||||||||||||||||||
| Definitions of various process capability indices |
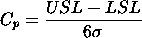
![Cpk = MIN[(USL-mu)/(3*sigma), (mu-LSL)/(3*sigma)]](http://www.itl.nist.gov/div898/handbook/pmc/section1/eqns/cpkdef.gif)

|
||||||||||||||||||||
| Sample estimates of capability indices |
Sample estimators for these indices are given below.
(Estimators are indicated with a "hat" over them).
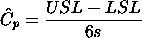
![Chat(pk) = MIN[(USL-m)/(3*s), (m-LSL)/(3*s)]](http://www.itl.nist.gov/div898/handbook/pmc/section1/eqns/cpkdef2.gif)
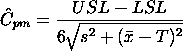
The estimator for Cpk can also be expressed as Cpk = Cp(1-k), where k is a scaled distance between the midpoint of the specification range, m, and the process mean, 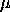 . .
Denote the midpoint of the specification range by m = (USL+LSL)/2. The distance between the process mean, 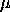 , and the optimum, which
is m, is , and the optimum, which
is m, is 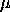 - m,
where - m,
where 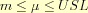 .
The scaled distance is .
The scaled distance is
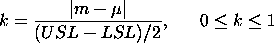
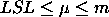 ). To determine
the estimated value, ). To determine
the estimated value,
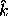 , we estimate , we estimate
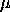 by by
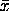 . Note that . Note that
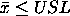 . .
The estimator for the Cp index, adjusted by the k factor, is 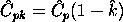
 ,
it follows that ,
it follows that 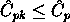 . .
|
||||||||||||||||||||
| Plot showing Cp for varying process widths |
To get an idea of the value of the Cp statistic for
varying process widths, consider the following plot
|
||||||||||||||||||||
| Translating capability into "rejects" |
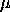 . .
We have discussed the situation with two spec. limits, the USL and LSL. This is known as the bilateral or two-sided case. There are many cases where only the lower or upper specifications are used. Using one spec limit is called unilateral or one-sided. The corresponding capability indices are |
||||||||||||||||||||
| One-sided specifications and the corresponding capability indices |
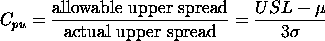
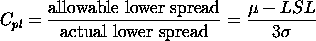
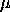 and and
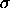 are
the process mean and standard deviation, respectively.
Estimators of Cpu and Cpl are obtained
by replacing are
the process mean and standard deviation, respectively.
Estimators of Cpu and Cpl are obtained
by replacing 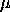 and and
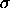 by by
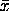 and s, respectively. The following relationship holds
and s, respectively. The following relationship holds
Cp = (Cpu + Cpl) /2.This can be represented pictorially by 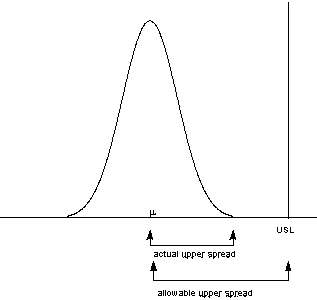
|
||||||||||||||||||||
| Confidence Limits For Capability Indices | |||||||||||||||||||||
| Confidence intervals for indices |
Assuming normally distributed process data, the distribution of the
sample
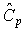 follows from a Chi-square distribution and
follows from a Chi-square distribution and
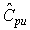 and
and
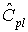 have distributions related to the non-central t distribution.
Fortunately, approximate confidence limits related to the normal
distribution have been derived. Various approximations to the
distribution of
have distributions related to the non-central t distribution.
Fortunately, approximate confidence limits related to the normal
distribution have been derived. Various approximations to the
distribution of
100(1- 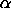 )%
Confidence Limits for Cp )%
Confidence Limits for Cp
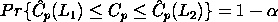  ν = degrees of freedom.
ν = degrees of freedom.
|
||||||||||||||||||||
| Confidence Intervals for Cpu and Cpl |
Approximate 100(1-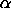 )%
confidence limits for Cpu with sample size n are: )%
confidence limits for Cpu with sample size n are:
![C(pu)(lower) = Chat(pu)-z(1-beta)*SQRT[(1/(9*n))+Chat(pu)^2/(2*(n-1))]](http://www.itl.nist.gov/div898/handbook/pmc/section1/eqns/cpulow.gif)
![C(pu)(upper) = Chat(pu)+z(1-alpha)*SQRT[(1/(9*n))+Chat(pu)^2/(2*(n-1))]](http://www.itl.nist.gov/div898/handbook/pmc/section1/eqns/cpuupp.gif)
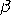 is
not known, set it to is
not known, set it to
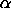 .
Limits for Cpl are obtained by replacing .
Limits for Cpl are obtained by replacing
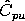 by by
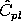 . .
|
||||||||||||||||||||
| Confidence Interval for Cpk |
Zhang et al. (1990)
derived the exact variance for the estimator of
Cpk as well as an approximation for
large n. The reference paper is Zhang, Stenback and Wardrop (1990),
"Interval Estimation of the process capability index", Communications
in Statistics: Theory and Methods, 19(21), 4455-4470.
The variance is obtained as follows:
Let ![c = SQRT(n)*[mu - (USL+LSL)/2]*sigma](http://www.itl.nist.gov/div898/handbook/pmc/section1/eqns/cpvar1.gif)
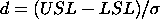
![Phi(-c) = integral[-infinity to -c][(1/(SQRT(2(*PI))*EXP(-5*z**2 dz]](http://www.itl.nist.gov/div898/handbook/pmc/section1/eqns/cpvar3.gif)
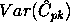
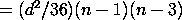
![-(d/(9*SQRT(n))*(n-1)*(n-3)*{SQRT(2*PI)*
EXP(-c**2/2) + c[1 - 2*PHI(-c)]}](http://www.itl.nist.gov/div898/handbook/pmc/section1/eqns/cpvar6.gif)
![+[(1/9)*(n-1)/(n*(n-3))]*(1+c**2)](http://www.itl.nist.gov/div898/handbook/pmc/section1/eqns/cpvar7.gif)
![-[(n-1)/(72n)]*{(GAMMA((n-1)/2))/(GAMMA((n-1)/2))}**2](http://www.itl.nist.gov/div898/handbook/pmc/section1/eqns/cpvar8.gif)
![*{d*SQRT(n) - 2*SQRT(2*PI)*EXP(-c**2/2) -
2*c*[1 - 2*PHI(-c)]}**2](http://www.itl.nist.gov/div898/handbook/pmc/section1/eqns/cpvar9.gif)
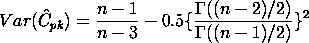 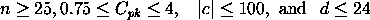 ![C(pk) = Chat(pk) +/- z(1-alpha/2)*SQRT[(1/(9*n)) + Chat(pk)^2/(2*(n-1))]](http://www.itl.nist.gov/div898/handbook/pmc/section1/eqns/cpkvar3.gif)  100 for
capability studies. Another point to observe is that
variations are not negligible due to the randomness of capability
indices. 100 for
capability studies. Another point to observe is that
variations are not negligible due to the randomness of capability
indices.
|
||||||||||||||||||||
| Capability Index Example | |||||||||||||||||||||
| An example |
For a certain process the USL = 20 and the LSL = 8. The observed
process average,
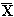 = 16, and the
standard deviation, s = 2. From this we obtain = 16, and the
standard deviation, s = 2. From this we obtain
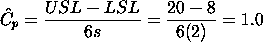  = 16. The = 16. The
 factor is
found by factor is
found by
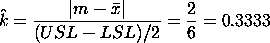 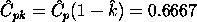 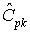 at least 1.0,
so this is not a good process. If possible, reduce the variability
or/and center the process. We can compute the at least 1.0,
so this is not a good process. If possible, reduce the variability
or/and center the process. We can compute the
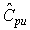 and
and
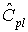
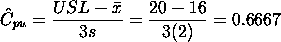
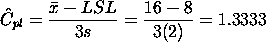
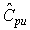 , which is the
smallest of the above indices, is 0.6667. Note that the formula , which is the
smallest of the above indices, is 0.6667. Note that the formula
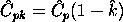 is the algebraic equivalent of the
min{
is the algebraic equivalent of the
min{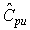 , ,
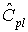 } definition. } definition.
|
||||||||||||||||||||
| What happens if the process is not approximately normally distributed? | |||||||||||||||||||||
| What you can do with non-normal data |
The indices that we considered thus far are based on normality of the
process distribution. This poses a problem when the process distribution
is not normal. Without going into the specifics, we can list some
remedies.
| ||||||||||||||||||||
Sunday, February 9, 2014
Process Capability
Subscribe to:
Post Comments (Atom)
-
Heavy Metals S 31 HEAVY METALS This test is provided to demonstrate that the content of metallic impurities...
-
Instrumentation HPLC systems HPLC instrumentation includes a pump, injector, column, detector and recorder or data system, connected as...
![Chatnpk = min[(USL - median)/(p(0.995) - median),
(median - LSL)/(median - p(0.005))]](http://www.itl.nist.gov/div898/handbook/pmc/section1/eqns/cnpk.gif)
No comments:
Post a Comment